UTS Semester 1 Matematika Diskrit

Nama:Sinta

Jurusan: Sistem Informasi

Kelas: Pagi

1. Gambarkan graf sederhana, memuat sisi rangkap dan memuat loop dengan 5 simpul dan 8 sisi

Jawaban :

Contoh graf sederhana

Graf di atas memiliki $5$ simpul, yaitu $A, B, C, D$ , dan $E$ . Graf itu memiliki $8$ sisi (dapat dihitung dari jumlah garis yang ada), yaitu sisi $A B$ , $A C$ , $A E$ , $B C$ , $B E$ , $C D$ , $C E$ , dan $D E$ . Graf itu sederhana karena tidak memiliki sisi rangkap maupun loop.

Jawaban b)

Contoh graf sederhana memuat sisi rangkap dan memuat loop dengan 5 simpul dan 8 sisi .

Perhatikan bahwa sisi penghubung $A B$ ada sebanyak $3$ sisi sehingga disebut sisi rangkap (multiple edges) dan $C C$ merupakan gelang (loop).

2. Misalkan G adalah graf dengan barisan derajat: (4, 3, 2, 1). Tentukan banyaknya sisi di G dan gambarkan graf G.

JAWABAN:

Menurut Lema Jabat Tangan (Handshaking Lemma), jumlah derajat titik pada suatu graf sama dengan $2$ kali banyak sisi. Diketahui bahwa jumlah derajat titik-titik graf itu adalah $4 + 3 + 2 + 1 = 10$ . Dengan demikian, banyak sisi di $G$ adalah $\frac{1}{2} \times 10 = 5$ . Gambar graf $G$ dapat dilihat sebagai berikut.

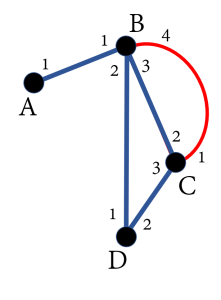
Tampak pada gambar di atas bahwa derajat titik $A, B, C$ , dan $D$ berturut-turut adalah $1, 4, 3$ , dan $2$ Tampak pula ada $5$ sisi pada graf tersebut.

3. Untuk setiap graf berikut, tentukan:

a. himpunan simpulnya;

b. himpunan sisinya.

c. derajat masing masing simpul

d. derajat maksimimum dari graf tersebut

e. derajat minimum dari graf tersebut

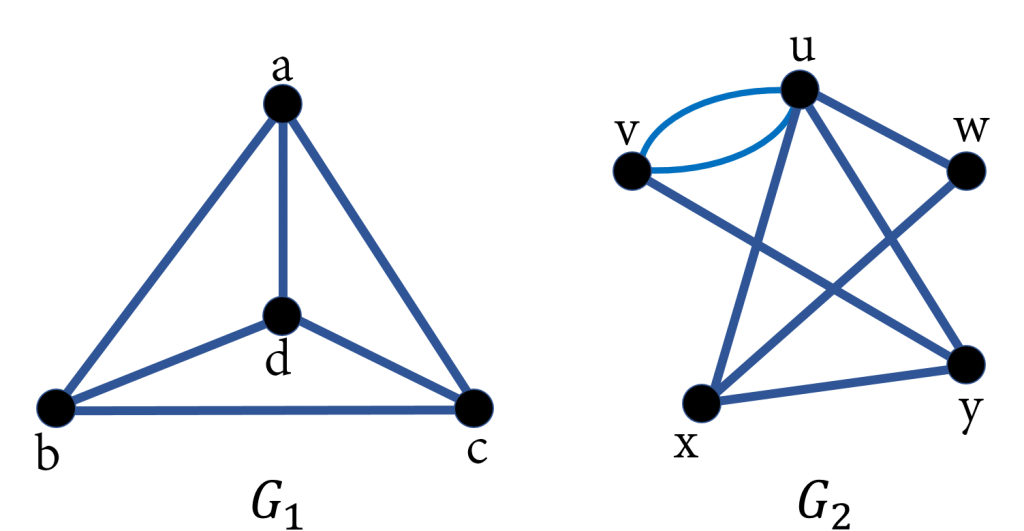
JAWABAN :

Jawaban a) Himpunan simpel graf $G$ kita notasikan dengan $V (G)$ , huruf $V$ diambil dari kata “Vertex”. Dari gambar, masing-masing graf telah diberi nama $G_{1}$ , $G_{2}$ , dan $G_{3}$ . Untuk itu, dapat kita tuliskan:
$V (G_{1}) = {a, b, c, d}$
$V (G_{2}) = {u, v, w, x, y}$
$V (G_{3}) = {1, 2, 3, 4, 5, 6}$

Jawaban b)

Himpunan sisi graf $G$ kita notasikan dengan $E (G)$ , huruf $E$ diambil dari kata “Edge”. Dari gambar, masing-masing graf telah diberi nama $G_{1}$ , $G_{2}$ , dan $G_{3}$ . Untuk itu, kita dapat tuliskan:
$E (G_{1}) = {a b, a c, b c, a d, b d, c d}$
$E (G_{2}) = {x y, x w, x u, v y, u w, u y, v u, v u}$
$E (G_{3}) = {12, 22, 23, 24, 25, 26, 45, 46}$